أسس المنطق الرّقمي: أنظمة العد Number Systems
مقدمة: الأرقام الثنائية، لغة الحاسوب المُميزة
في عالم الحواسيب والأنظمة الرقمية، يتم التعامل مع المعطيات والبيانات وفقاً لتمثيلٍ وطريقةٍ خاصة. هنا علينا أن نتذكر أمراً هام، وهو أن الدارات الحاسوبية المسؤولة عن معالجة المعطيات، وتخزينها، ونقلها، وحتى إرسالها لوحدات الإظهار، لا تستطيع أن تفهم إلا نمطاً واحداً من المعطيات: المعطيات الثنائية، أي المعطيات التي تكون على شكل سلاسل من الأصفار والواحدات. بمعنى آخر، فالحاسوب يمتلك لغته الخاصة، التي تتخاطب أجزائه عبرها، وكي يستطيع فهم الأوامر التي نرسلها إليه باللغة التي نفهمها نحن، يجب أن يتم تحويل المعلومات والمعطيات إلى لغته الخاصة به، ودون ذلك، لن يستطيع الحاسوب تنفيذ عمليات المعالجة وأي نمط آخر من الأوامر قد نطلبها منه.
بهذا السياق، فإن التعامل مع الحواسيب والأنظمة الرقمية يتطلب معرفة بأنظمة أعداد معينة، تختلف قليلاً عن أنظمة الأعداد التي نتعامل معها بالحياة اليومية، ولكنها ترتبط بها، حيث يمكن التحويل من هذه الأنظمة إلى النظام الذي نفهمه بحياتنا اليومية، والعكس أيضاً صحيح.
من ناحيةٍ أخرى، وبما أن العمليات التي تجري ضمن الدارات الحاسوبية والأنظمة الرقمية تعتمد على الجبر البولياني، فإن الأعداد التي سيتم التعامل معها يجب أن تخضع أيضاً لشروط الجبر البولياني، وأي نمط معلومات يتم إدخاله للحاسوب، يجب أن يتم تحويله للصيغ التي يفهمها الجبر البولياني، كي تتمكن الدارات الحاسوبية من التعامل معها، ومعالجتها، ومن ثم تقوم بإعادة تحويلها للنمط الذي نفهمه نحن كبشر.
إذاً، فإننا سنستعرض ضمن هذه المقالة أنظمة العد التالية، والتي تعتبر حجر أساس لأي شخص يريد الدخول لعالم الأنظمة الرقمية والدارات الحاسوبية:
1- نظام الأعداد العشري Decimal System
2- نظام الأعداد الثنائي Binary System
3- نظام الأعداد الثماني Octal System
4- نظام الأعداد الستة عشري Hexa-Decimal System
يجدر بنا التنويه هنا إلى أمرٍ هام جداً، وهو أساسيات أي نظام أعداد، فكل نظام أعداد يتصف بشكلٍ أساسي بما يلي:
- أساس النظام: وسنعطيه المتحول (n)
- مكونات النظام: وهي الأعداد من (0) وحتى (n-1)
بناءً على الأساسيات البسيطة السابقة، أصبح الآن بإمكاننا البدء بتوضيح أنظمة العد ودورها في العالم الرقمي، ومن نظام الأعداد العشري سنبدأ…
نظام الأعداد العشري Decimal System
نظام الأعداد العشري هو أبسط أنظمة العد من حيث سهولة الفهم لنا كبشر. فهو نظام الأعداد الذي نستخدمه في الحياة اليومية، والذي نستطيع تطبيق عليه العمليات الجبرية بالشكل التقليدي: أي الجمع والطرح والضرب والقسمة.
أساس النظام العشري هو العدد (10)، وبالتالي فإن مكوناته ستكون من (0) وحتى (10-1) أي من (0) وحتى (9). بالنسبة لنظام الأعداد العشري، فإن أي رقم فيه يمكن تمثيله باستخدام كثيرات الحدود. ومن دون الخوض بالتفاصيل، سنأخذ المثال التالي كي نفهم أكثر كيفية بناء العدد العشري.
ليكن لدينا العدد (843)، فإنه فعلياً عبارة عن مجموع جداءات كل عدد، مضروباً بالمرتبة العشرية الموافقة. فالعدد (8) سيكون مضروباً بالمرتبة العشرية الثانية، أي (10^2) وهي 100، والعدد (4) سيكون مضروباً بالمرتبة العشرية الأولى، أي (10^1) وهي العدد 10، أما العدد (3) فسيكون مضروباً بالمرتبة العشرية الصفرية، أي (10^0) وهي تساوي الواحد، ومع جمع الحدود السابقة، نستطيع الحصول على القيمة الكلية للعدد، وهي 843. تدعى المرتبة العشرية التي يتم الضرب بها بالـ “وزن”.

نظام الأعداد الثنائي Binary Number System
نظام الأعداد الثنائي، فعلياً، هو أساس الثورة الرقمية بالكامل، وأساس عمليات المعالجة الحاسوبية كلها. بشكلٍ بسيط، فإن هذا النظام يتألف من عددين فقط : 0 و 1. وبالتالي فإن أساس النظام هو (2) ومكونات النظام هي {0,1}.
كي تصبح الصورة أوضح، فإن أي نمط من أنماط المعلومات، يتم ترميزه في نظام الأعداد الثنائي باستخدام سلسلة من الأصفار والواحدات. فكر بأي نمط من أنماط المعلومات: حرف، كلمة، صورة، فيديو، كلها يتم تمثيلها في نظام الأعداد الثنائي باستخدام سلاسل طويلة من الأصفار والواحدت، ولا شيء سواها.
تكمن أهمية النظام الثنائي، من كونه نظام الترميز المستخدم لتمثيل المعلومات والمعطيات ضمن الدارات الحاسوبية والرقمية، فأي معلومة، يتم تحويلها بشكلٍ أساسي إلى نظام الأعداد الثنائي، ومن ثم يتم تتم معالجتها ضمن الحاسوب، وأخيراً يتم تحويل ناتج المعالجة للشكل الذي نستوعبه، ويتم إظهاره. هذا – ببساطة – مبدأ عمل كافة الأجهزة الحاسوبية، بدءاً من الحواسيب المنزلية، إلى الحواسيب المحمولة، وصولاً للهواتف الذكية والحواسيب اللوحية.
بالطبع، هنالك قواعد للتحويل بين أنماط المعطيات والمعلومات لتصبح متناسبة مع النظام الثنائي، وكذلك طرق لتحويل المعلومات والمعطيات من النظام الثنائي إلى الأنماط الأخرى، لتصبح قابلةً للفهم والاستيعاب من قبلنا.
النظام الثنائي: البت والبايت Bit and Byte
في النظام الثنائي، فإن كل رقم فيه يعرف باسم “البت bit”، وهو اختصار لكلمة “رقم ثنائي Binary Digit”. البت، هو أصغر واحدة لترميز المعلومات في الحاسوب، وكل الواحدات الأخرى التي نستعملها يومياً هي من مضاعفات البت.
البايت Byte، هو عبارة عن سلسلة من (8) بتات، وبالتالي، فإن أي سلسلة من 8 أرقام ثنائية تمثل بايتاً واحداً. أيضاً، يتم استخدام مضاعفات واحدة البايت في الحياة اليومية من أجل تمثيل المعطيات والمعلومات. لنأخذ مثال توضيحي، ولنتخيل صورةً ذات حجم 512 كيلوبايت. ما الذي نقصده بأن حجم الصورة هو 512 كيلوبايت؟
في الواقع، فإن ما نقصده بالضبط، هو أن الصورة نفسها، والتي تضم طيفاً واسعاً من الألوان، والخطوط، وغيرها، قد تم ترميزها باستخدام مساحة قدرها 512 كيلوبايت، وبما أن البايت نفسه هو (8) بت، والكيلوبايت هو عبارة عن 1024 بايت، فهذا يعني أن الصورة التي يبلغ حجمها 512 كيلوبايت، قد تم ترميزها باستخدام عدد من الأصفار والواحدات يبلغ: 512*1024*8 = 4194304 بت! أي 4194304 عدد ثنائي! الآن يمكنكم أن تتخيلوا كمية الأصفار والواحدات الهائلة التي تتضمنها الذواكر الحالية والتي تبلغ بشكلٍ وسطي 1 تيرابايت من المعطيات!
ولكن، ما الذي يجعل النظام الثنائي مميزاً؟
الإجابة على السؤال السابق تنحصر كما يلي: أولاً، يمكن عبر النظام تمثيل أي عدد من أي نظام عددي (وهو ما سنأتي على توضيحه). ثانياً، النظام الثنائي هو النظام العددي الذي يمكن تطبيق قواعد الجبر البولياني عليه بشكلٍ مباشر، وبالتالي تنفيذ كافة العمليات المنطقية اللازمة من أجل تكوين الدارات الحاسوبية والرقمية. هذا الأمر، هو ما جعل نظام الأعداد الثنائي أساس الثورة الرقمية، وأساس نظم ترميز المعلومات.
نظام الأعداد الثماني Octal Number System
نظام الأعداد الثماني هو نظام الأعداد الذي أساسه العدد (8)، وهذا يعني أن مكونات هذا النظام ستكون: {0,1,2,3,4,5,6,7}. لا يستخدم نظام الأعداد الثماني بكثرةٍ في أيامنا هذه، واقتصرت استخداماته على البدايات الأولى لظهور الحواسيب.
نظام الأعداد الستة عشري Hexadecimal Number System
يمتلك نظام الأعداد الستة عشري أساساً هو العدد (16)، وبالتالي فإن مكونات هذا النظام هي الأعداد التالية: {0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}. وبهدف التمييز بينه وبين النظام العشري، تم ترميز الأرقام من 10 وحتى 15 في النظام الستة عشري بالأحرف التالية: A, B, C, D, E, F حيث تشير هذه الأحرف للأرقام 10,11,12,13,14,15 على التوالي.
التحويل بين أنظمة العد
قبل الحديث عن استخدامات أنظمة العد، يجب أن نعلم أمراً هاماً حولها: يمكن التحويل بين أنظمة العد وبسهولة، وذلك وفقاً لقواعد معينة. الهدف من عملية التحويل هذه هو نقل المعطيات من الصيغ التي نتعامل معها ونفهمها مباشرةً (مثل النظام العشري) إلى الصيغ التي يتعامل معها الحاسوب ويفهمها (مثل النظام الستة عشري والنظام الثنائي). وبالعودة للجبر البولياني، فإننا سنجد مثلاً أن تنفيذ العمليات الرياضية التابعة للجبر البولياني لا يمكن أن يتم إلا على المعطيات المنطقية التي تحمل أحد حالتين: الحالة الصحيحة True أو الحالة الخاطئة False، وبالنظر لأنظمة العد، فإننا نستطيع أنه لا يوجد نظام عد متوافق مع هذه العمليات إلا النظام الثنائي، فعبر إسناد قيمة “1” للحالة الصحيحة، وقيمة “0” للحالة الخاطئة، أصبح بإمكاننا تنفيذ العمليات الرياضية في الجبر البولياني وبالشكل الكامل.
ينبغي لنا أن نقول أننا لن نستعرض كافة المفاهيم المتعلقة بالتحويل بين أنظمة العد بشكلٍ مفصل، بل سنكتفي بالإشارة لأهم ما يتعلق بها، وإعطاء بعض الأمثلة التوضيحية عنها.
1- عمليات التحويل الخاصة بالنظام العشري
بالنسبة للنظام العشري، فإن عملية تحويل أي عدد بالنظام العشري، إلى العدد الموافق له بنظام عد آخر، هي أسهل عمليات التحويل، حيث تتم بالتقسيم على أساس النظام، مع أخذ باقي القسمة بعين الاعتبار. فلو أردنا التحويل من النظام العشري للنظام الثنائي، نأخذ الرقم العشري المراد تحويله، ونقوم بتقسيمه على العدد “2”، وذلك حتى تصبح عملية القسمة غير ممكنة، ومن ثم نقوم بأخذ باقي القسمة من الأسفل للأعلى، ونحصل بالتالي على العدد العشري ممثلاً بالنظام الثنائي. هذا المفهوم ينطبق أيضاً على النظام الثماني والستة عشري وبنفس الطريقة تماماً.
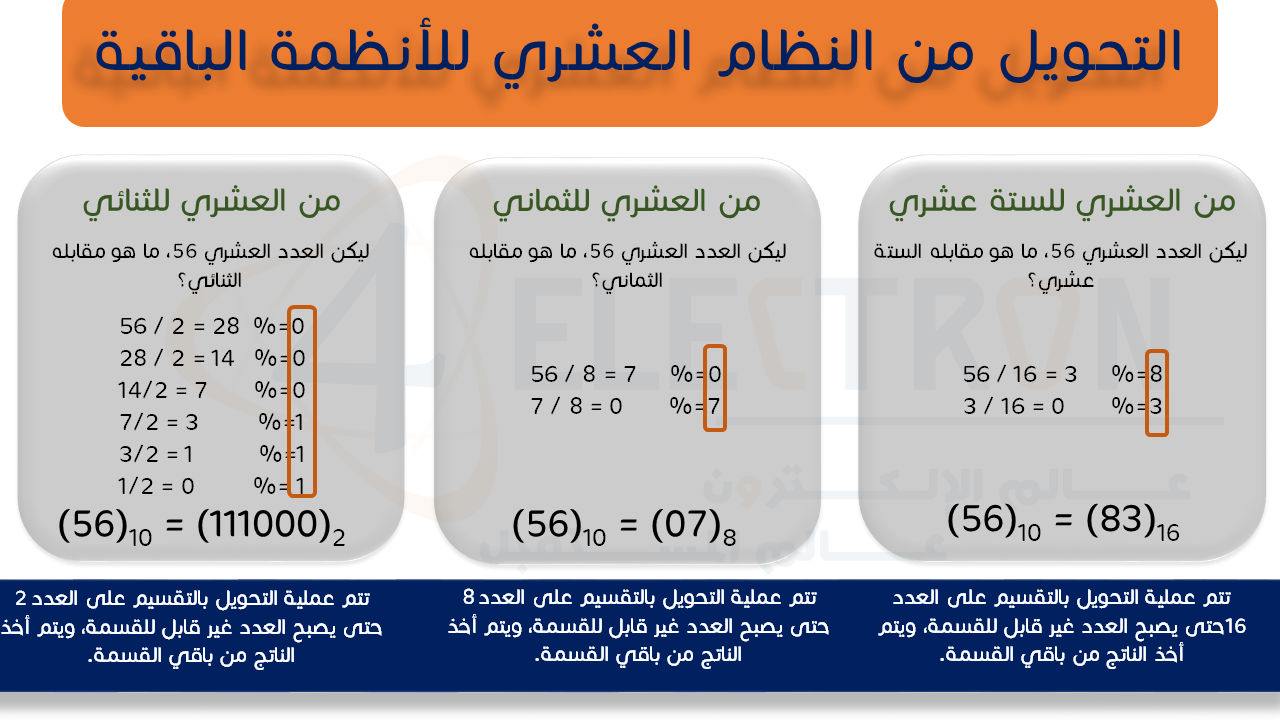 هنالك ملاحظة هامة هنا، وهي أنه على الرغم من أن الأرقام المستخدمة في النظامين الثماني والستة عشري، هي مشابهة للأرقام في النظام العشري، إلا أنها ليست نفسها! فالرقم (56) الثماني ليس نفسه (56) العشري، والرقم (56) الستة عشري ليس نفسه (56) العشري أو حتى (56) الثماني. توضيح هذه النقطة سيكون عند الحديث عن علاقة النظام الثنائي بالأنظمة الأخرى.
هنالك ملاحظة هامة هنا، وهي أنه على الرغم من أن الأرقام المستخدمة في النظامين الثماني والستة عشري، هي مشابهة للأرقام في النظام العشري، إلا أنها ليست نفسها! فالرقم (56) الثماني ليس نفسه (56) العشري، والرقم (56) الستة عشري ليس نفسه (56) العشري أو حتى (56) الثماني. توضيح هذه النقطة سيكون عند الحديث عن علاقة النظام الثنائي بالأنظمة الأخرى.
الآن، علينا توضيح كيفية الانتقال من أحد الأنظمة للنظام العشري. وهنا علينا تذكر أمر هام جداً، وهو كيفية ترميز النظام العشري، وقد قلنا سابقاً أن النظام العشري هو نظام الأعداد الذي يتم التعبير عن أي عددٍ فيه باستخدام مبدأ كثيرات الحدود Polynomials. الآن، ومن أجل تحويل أي عدد للنظام العشري، فإن كل ما علينا القيام به هو استخدام قاعدة كثيرات الحدود، مع استبدال أساس القوة التي نضرب بها، بأساس النظام العددي نفسه، فإذا كان الرقم المراد تحويله بالنظام الثنائي، فإن أساس قوة العدد سيكون (2)، وإذا كان العدد بالنظام الثماني، فإن أساس القوة هو (8)، وإذا كان بالنظام الستة عشري، فإن أساس القوة هو العدد (16). وسنستخدم نفس المثال السابق، ولكن معكوساً، أي أننا نريد استخدام الأعداد السابقة من أجل معرفة مقابلها العشري.
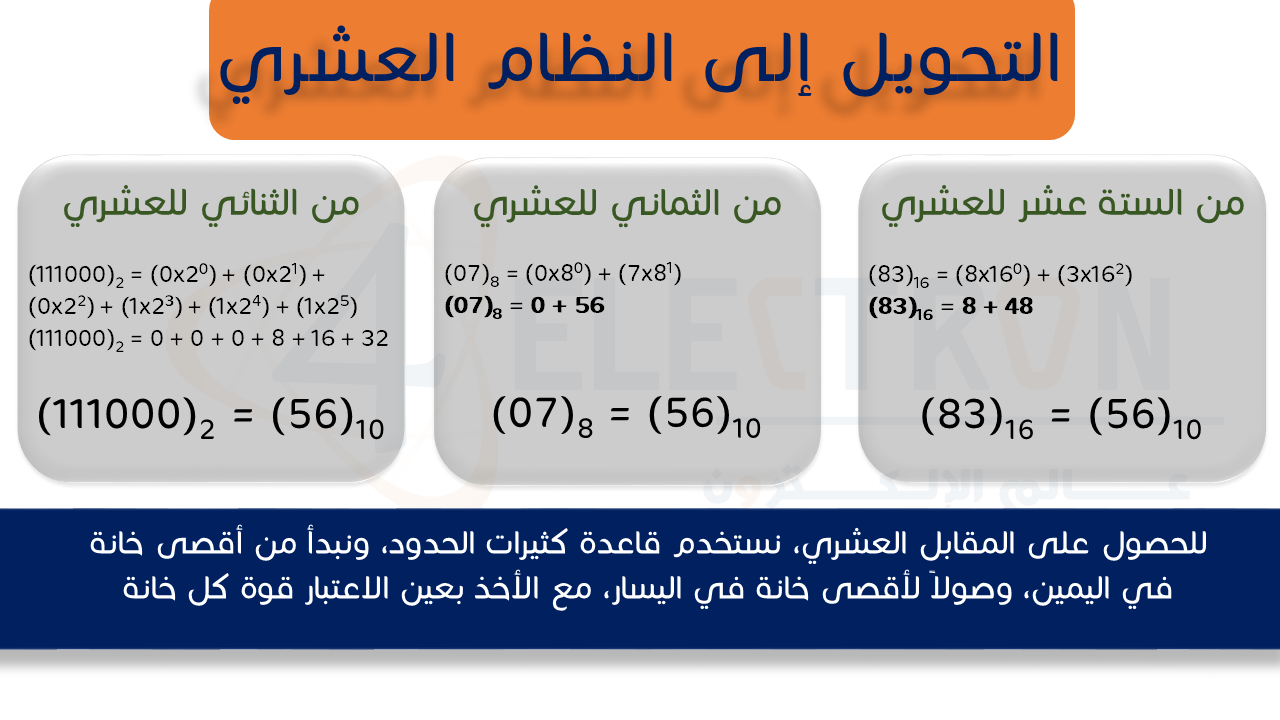 2- التحويل من وإلى النظام الثنائي
2- التحويل من وإلى النظام الثنائي
بدأنا توضيحنا لعمليات التحويل بالنظام العشري، لأنه يمثل النظام العددي المألوف بالنسبة لنا، والذي يمكن أن تطبق عليه العمليات الجبرية كما نعرفها. الآن، سننتقل لتوضيح كيفية التحويل إلى نظام الأعداد الثنائي وبالعكس.
من أجل التحويل للنظام الثنائي، علينا تذكر أن النظام الثنائي يتكون من عددين فقط: الصفر “0” والواحد “1”، ويمكن التعبير عن أي رقمٍ من أي نظام عددي بالنظام الثنائي، عبر سلسلةٍ من الأعداد الثنائية. تدعى أقصى خانة من اليمين ضمن السلسلة الثنائية بالـ “البت الأقل أهمية LSB” بينما تدعى أقصى خانة من اليسار بالـ “البت الأكثر أهمية MSB”. على سبيل المثال، فإن العدد العشري (45) يتم تمثيله بالنظام الثنائي بالسلسلة (101101). كيف يتم ذلك؟ علينا أن نتذكر أن العدد العشري يتم ترميزه باستخدام مبدأ كثيرات الحدود، وبناءً عليه، فإن كل خانة ضمن السلسلة الثنائية الممثلة للعدد العشري سيكون لها “وزن”. وزن الخانة الثنائية يمثل القيمة الموضوعة فيها (صفر أو واحد) مضروبةً بالعدد 2 (أساس نظام العد) مرفوعاً للأس الموافق لترتيب الخانة. وفي حين أن الترتيب يبدأ من أقصى اليمين، فإن العدد الموضوع في الخانة ذات الترتيب “0” سيأخذ القوة (0)، والخانة التي تليها ستكون ذات معامل قوة قدره (1)، والتي تليها ستكون ذات معامل قدره (2)، وهكذا قدر ما نشاء. الآن، كيف نقوم بحساب السلسلة الثنائية الموافقة؟ حسناً، سنأخذ مثالاً وليكن العدد (45) العشري، ونريد أن نقوم بحساب الموافق العشري له. ما علينا القيام به هو اتباع الخطوات التالية:
- نقوم بكتابة سلسلة عددية، أساسها العدد (2)، وكل حد يختلف فيها عن الحد الذي يسبقه بقيمة الأس. تبدأ هذه السلسلة بالعدد (2) مرفوعاً للأس (القوة) صفر، وتستمر قدر ما نشاء. فعلياً، يجب أن تتوقف السلسلة عند اقتراب قيم خاناتها من العدد العشري المطلوب تحويله.
- نقوم بحساب قيمة كل خانة من خانات هذه السلسلة.
- ننظر لقيمة الأعداد المكونة للسلسلة، ونبحث عن الخانات التي مجموع قيمها سيساوي (45). نبدأ عملية جمع قيم الخانات بدءاً من اليسار إلى اليمين.
- كل خانة تم استخدام قيمتها نعطيها الرقم “1”، وكل خانة لم يتم استخدام قيمتها نعطيها الرقم “0”. الآن نقوم بترتيب الواحدات والأصفار بدءاً من اليسار إلى اليمين، فنحصل على العدد الثنائي المطلوب.
هل وجدتم الكلام السابق معقداً وصعباً للفهم؟ حسناً، الصورة التالية تظهره وتوضحه كاملاً وبشكلٍ بسيط. الخانات التي نحتاجها لتشكيل العدد (45) تم إحاطتها بالمستطيل البرتقالي، بينما الخانات التي لم يتم استخدامها تم إحاطتها بالمستطيل الأزرق. كان بالإمكان وضع الخانة الموافقة للعدد (2) مرفوعاً للقوة (6) والتي تساوي القيمة (64)، ولكنها ستأخذ القيمة “0”، وقيمة “0” على اليسار تعتبر قيمةً مهملة، لذلك تم اعتماد الخانة الموافقة للعدد (2) مرفوعاً للقوة (5) كأعلى قيمة مطلوبة لتشكيل العدد (45)، بالإضافة للخانات الثنائية الأخرى.
 بالنسبة للنظام الثماني، فإنه يمكن ترميز أي رقم بالنظام الثماني باستخدام (3) أعداد ثنائية، أما بالنسبة للنظام الستة عشري، فإنه يمكن تمثيل أي رقم فيه باستخدام (4) خانات بالنظام الثنائي. لماذا؟ لنتذكر أن العدد 2 مرفوعاً للقوة (3) هو (8)، وبالتالي، فإنه وباستخدام (3) خانات ثنائية، سيكون بالإمكان ترميز (8) أعداد، وهو المطلوب بحالة النظام الثماني. أما بالنسبة للنظام الستة عشري، فإننا يجب أن نتذكر أن 2 مرفوعاً للقوة 4 هو 16، وهذا يعني أنه باستخدام 4 خانات ثنائية نستطيع ترميز 16 قيمة، وهو المطلوب بالنسبة للنظام الستة عشري. هنا يجدر بنا الإشارة لنقطةٍ هامة، وهي أن كل عدد ثماني يحتاج لـ 3 خانات ثنائية، وهذا يعني أننا لكتابة رقم ثماني يتكون من خانتين، سنكون بحاجة لثلاث خانات لكل عدد، أي 6 خانات ككل. ولو كان العدد الثماني يتكون من 3 خانات، فإننا سنحتاج لـ 9 خانات ثنائية لترميز العدد، وهكذا. الأمر نفسه ينطبق على النظام الستة عشري، الذي يتطلب ترميز كل خانة فيه 4 خانات ثنائية، وبالتالي فإن عدداً بالنظام الستة عشري يتكون من 3 خانات مثلاً، سيتطلب 12 خانة ثنائية كي يتم ترميزه.
بالنسبة للنظام الثماني، فإنه يمكن ترميز أي رقم بالنظام الثماني باستخدام (3) أعداد ثنائية، أما بالنسبة للنظام الستة عشري، فإنه يمكن تمثيل أي رقم فيه باستخدام (4) خانات بالنظام الثنائي. لماذا؟ لنتذكر أن العدد 2 مرفوعاً للقوة (3) هو (8)، وبالتالي، فإنه وباستخدام (3) خانات ثنائية، سيكون بالإمكان ترميز (8) أعداد، وهو المطلوب بحالة النظام الثماني. أما بالنسبة للنظام الستة عشري، فإننا يجب أن نتذكر أن 2 مرفوعاً للقوة 4 هو 16، وهذا يعني أنه باستخدام 4 خانات ثنائية نستطيع ترميز 16 قيمة، وهو المطلوب بالنسبة للنظام الستة عشري. هنا يجدر بنا الإشارة لنقطةٍ هامة، وهي أن كل عدد ثماني يحتاج لـ 3 خانات ثنائية، وهذا يعني أننا لكتابة رقم ثماني يتكون من خانتين، سنكون بحاجة لثلاث خانات لكل عدد، أي 6 خانات ككل. ولو كان العدد الثماني يتكون من 3 خانات، فإننا سنحتاج لـ 9 خانات ثنائية لترميز العدد، وهكذا. الأمر نفسه ينطبق على النظام الستة عشري، الذي يتطلب ترميز كل خانة فيه 4 خانات ثنائية، وبالتالي فإن عدداً بالنظام الستة عشري يتكون من 3 خانات مثلاً، سيتطلب 12 خانة ثنائية كي يتم ترميزه.
3- العلاقة بين النظام الثنائي والنظامين الثماني والستة عشري
بعد أن تعرفنا على كيفية التحويل بشكلٍ مباشر بين النظامين الثنائي والعشري، علينا أن نسلط الضوء على العلاقة بين النظام الثنائي والثماني، والنظام الثنائي والنظام الستة عشري.
بالبداية، علينا أن نتذكر أن العدد (8) هو عبارة عن (2^3)، والعدد (16) هو عبارة عن (2^4)، وبالتالي، وعبر هذا المفهوم البسيط، تصبح العلاقة واضحة وسهلة:
كل عدد في النظام الثماني يمكن تمثيله عبر ثلاثة أعداد ثنائية، وكل عدد في النظام الستة العشري يمكن تمثيله عبر أربعة أعداد ثنائية.
كمثال توضيحي بسيط، فإن العدد (0) في النظام الثماني، يكتب باستخدام النظام الثنائي عبر السلسلة (000)، والعدد (0) في النظام الستة عشري، يكتب في النظام الثنائي عبر السلسلة (0000). بينما العدد (1) الثماني، فإنه يكتب ثنائياً باستخدام السلسلة (001)، والعدد (1) في النظام الستة عشري يكتب ثنائياً باستخدام السلسلة (0001). يمكن تلخيص هذه المفاهيم كاملةً باستخدام الجدول التالي البسيط.
الجدول السابق يعطينا فكرة جيدة وتصور ممتاز حول أنظمة العد والعلاقة فيما بينها. فالنظام العشري هو النظام الذي نألفه ونتعامل معه، بينما النظام الثنائي هو النظام الذي يتكون فقط من عددين (0,1) ويمكن تمثيل أي عدد عبر سلسلة من الأعداد الثنائية. النظام الثنائي هو نظام أساسه العدد (8) ومكوناته هي (0,1,2,3,4,5,6,7) ونلاحظ أن العدد التالي بعد العدد (07) في النظام الثماني سيكون (11) وليس (08) مثلاً، وذلك لأن الرقم (8) ليس ضمن مكونات النظام، وكذلك الرقم (9). نفس الأمر بالنسبة للنظام الستة عشري، فأساسه العدد (16) ومكوناته هي من (0) وحتى (15)، وللتفريق بين أعداده وأعداد النظام العشري، تم ترميز الأعداد من (10) وحتى (15) بالأحرف (A,B,C,D,E,F) على التوالي. نلاحظ أن العدد التالي بعد العدد (15) في النظام الستة عشري هو (11)، أي بداية تعداد جديد، وليس العدد (16)، لأن العدد 16 ليس ضمن مكونات النظام. كنتيجة، فإن كل نظام أعداد يقوم بتكرار نفسه بعد انتهاء مكوناته، ولكننا ننتقل لخانةٍ جديدة. فبعد انتهاء أول ثمانية أعداد من النظام الثماني، فإننا نقوم بتكرارها، ولكن ضمن خانة (1)، بدلاً من خانة (0) التي تم البدء بها، وعند انتهاء المكونات الثمانية المرتبطة الرقم (1) يعيد النظام نفسه ولكن مع خانة (2) وهكذا، ونفس الأمر ينطبق تماماً على النظام الستة عشري.
الأمر الثاني الهام الذي نلاحظه من الجدول، هو أن كل رقم ثماني يمكن ترميزه باستخدام (3) أعداد ثنائية، وكل رقم ستة عشري يمكن ترميزه باستخدام (4) خانات ثنائية. فالعدد الثماني (10) مثلاً، يقابل بالجدول العدد الثنائي (1000)، ولو نظرنا له، فالعدد (10) مكون من رقمين: 0 و 1. العدد 0 يأخذ الخانات الثنائية الثلاثة الأولى من اليمين لليسار وهي (000)، والعدد 1 يأخذ الخانات الباقية. طبعاً، وكي يكون العدد (10) مرمزاً بشكل صحيح بالنظام الثنائي، فإنه يجب أن يتكون من (6) خانات، والأمر هنا بسيط جداً، فكل ما علينا القيام به هو إضافة عدد مناسب من الأصفار على اليسار، حتى يصبح العدد الثماني مرمزاً بشكل صحيح ثنائياً. كنتيجة، فإن المقابل الثماني للعدد (10)، هو (001000). الخانات الثلاث الأولى من اليمين (000) تقابل العدد (0) الثماني، والخانات الثلاث التالية (001) تقابل العدد (1). هذا الأمر ينطبق على كل الأعداد الثمانية. بالنسبة للأعداد الستة عشرية، فإن الطريقة نفسها تنطبق، ولكن على أربعة خانات: أي أن كل عدد ستة عشري يجب أن يتكون من أربعة خانات ثنائية.
يمكن فهم العلاقات السابقة باستخدام المثال التالي: سنأخذ العدد العشري (20)، وسنوجد مقابله الثنائي، والثماني، والستة عشري، وذلك عبر الصورة التوضيحية التالية:
 إلى هنا، نكون قد غطينا كافة المواضيع الأساسية المتعلقة بأنظمة العد، وأسسها، ومبادئ التحويل فيما بينها. هنالك مواضيع وقضايا إضافية تتعلق بالأعداد ذات الفاصلة وكيفية تمثيلها، أو إجراء العمليات الحسابية على أنظمة العد. بعض هذه القضايا سنتعرض لها في مقالاتٍ مقبلة، والبعض الآخر سنخصص لها مقالاتٍ منفصلة.
إلى هنا، نكون قد غطينا كافة المواضيع الأساسية المتعلقة بأنظمة العد، وأسسها، ومبادئ التحويل فيما بينها. هنالك مواضيع وقضايا إضافية تتعلق بالأعداد ذات الفاصلة وكيفية تمثيلها، أو إجراء العمليات الحسابية على أنظمة العد. بعض هذه القضايا سنتعرض لها في مقالاتٍ مقبلة، والبعض الآخر سنخصص لها مقالاتٍ منفصلة.
المصادر
1- كتاب “الإلكترونيات العملية للمبتكرين”.
2- “الدارات المنطقية“، تأليف الدكتور أحمد خضور، منشورات كلية الهندسة الميكانيكية والكهربائية، جامعة دمشق.
3- موسوعة ويكيبيديا بالإنجليزية: هنا و هنا و هنا و هنا
4- موسوعة بريتانيكا
5- موقع Rapid-Tables
6- موقع Electronic-Tutorials











يعطيك كل العافية
انا طالب هندسة كمبيوتر سينس في الهند
الدراسة في الانكليزي طبعا
انا يعني شبه مو فاهم شي بسب لغتي لانها ضعيفة وعم ابحث بالنت علا كتب بالعربي حتى تكون الدراسة اسهل شوي
يعني علا الاقل اكون فاهم محتوى الكتاب
ارجو المساعدة اذا بتعرف كتاب او موقع او مرجع بموادي او بمادة ال DLD digital logic design
ولكم جزيل الشكر ..
جزاكم الله خيرا ووفقكم لما فيه رضاه
شرح رائع وسهل
شكرا جزيلا
درسته بالمدرسة والجامعة اول مرة افهمها
يا أخي يوجد أخطاء قاتلة، لازم تتأكد من المعلومة قبل أن تحملها للنت و الناس تضرر.
الأخطاء عديدة أذكر منها مثال:
أنتم تكتبون انه: (٥٦) بالعشري = ( ٠٧ ) بالثماني وهذا غلط.
الصحيح: ( ٥٦ ) بالعشري = ( ٧٠ ) بالثماني .
.
سؤالي هو هل هناك طريقة تحويل مباشره من النظام الثماني الى الساذس عشر دون المرور بالثنائي