الجبر الخطي وعلاقته بالذكاء الاصطناعي

يُشكل مجال الجبر حجر الأساس في فهم نماذج الذكاء الاصطناعي وكيفية عملها، ويمكن فهم الذكاء الاصطناعي على أنه الحل الأمثل لمجموعة كبيرة من المعادلات الرياضية بمتغيراتٍ كثيرة

1. مقدمة في الجبر

 تتطلب دراسة وتطوير أي مجال علمي تقني الاتفاق على لغة ومفردات نستطيع من خلالها ترجمة المفاهيم والأفكار إلى أسس وقوانين موحدة يستطيع أي شخص مهتم فهمها ببساطة. هنا ندرك أهمية علوم الرياضيات، حيث أن هذا العلم يهدف إلى ترجمة الظواهر والأحداث إلى بضعة أرقام أو رموز رياضية أو معادلات لتسهيل شرحها وتفسيرها، ويوجد العديد من فروع الرياضيات التي تُساعدما على تدوين مُختلف الأحداث، مثل علم الحساب، اﻷرقام،  التحليل، الإحصاء، الهندسة الرياضية، الاحتمالات وغيرها.   

أحد الفروع الهامة في الرياضيات هو الجبر Algebra، الذي يوّفر لغةً أساسية لكتابة العلاقات بين مختلف المُتغيرات على شكل رموز رياضية بالإضافة لتوفير القدرة على صياغة مجموعة من القوانين والأساليب للتلاعب بتلك الرموز لكشف استنتاجات عن طريقة عمل تلك المتغيرات.

كيف نستطيع فهم ذلك؟ وما هي هذه “المتغيرات” التي يُساعدنا علم الجبر على تحويلها إلى رموزٍ ومعادلاتٍ قابلة للحساب؟ أبسط مثال يمكن التفكير به بهذا الخصوص هو الحركة ومعادلة حساب المسافة التي يقطعها جسم خلال فترةٍ زمنية معينة. عندما نتحدث عن جسمٍ يتحرك فإننا نستخدم كلمات ذات معنى شامل وغير دقيق، مثل: كانت السيارة تتحرك بسرعة، أو كانت السيارة بطيئة. ولكن ما الذي يعنيه “سريع” و “بطيء”؟ نحن نحتاج هنا إلى آلية تحدد بدقة المسافة التي قطعتها هذه السيارة خلال مدة زمنية معينة لنستطيع وصف حركة هذه السيارة بدقة.

• اقرأوا أيضاً: مقدمة في الذكاء الاصطناعي، تعلم الآلة والشبكات العصبونية

2. كيف يساعدنا الجبر على فهم العالم من حولنا: ظاهرة الحركة

هذا ما يوفره لنا علم الجبر الذي يحول هذه الظاهرة الفيزيائية – أي الحركة خلال مدة زمنية معينة – إلى رموزٍ رياضية بسيطة، عن طريق معادلة الحركة والتحريك التي يمكن عبرها حساب المسافة المقطوعة في زمن ثابت يساوي Δt على خط مستوي، حيث نستطيع كتابة تلك العلاقة على شكل d = v*Δt، حيث d يرمز للمسافة وv يرمز للسرعة. 

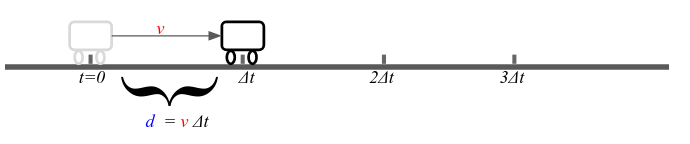
بفضل الجبر وبهذه البساطة نستطيع أن نعرف قيمة المسافة ﻷي سرعة كانت من خلال معادلة واحدة ذات متغير واحد v، وبشكلٍ مماثل، نستطيع عبر تعديل المعادلة معرفة السرعة في حال كنا نعلم المسافة المقطوعة خلال زمنٍ معين. بما أن قيمة السرعة في هذا المثال قد تتمثل بأي رقم على مستقيم اﻷعداد، نستطيع أن نقول أن المتغير v ينتمي إلى مجموعة اﻷعداد الحقيقية ℝ فنكتب v ∈ ℝ. واﻵن أصبحت لدينا المعلومات الكافية لمعرفة قيم السرعة وبالتالي ومن خلال المعادلة نستنتج قيم المسافة.

فإذا قمنا برسم العلاقة بين السرعة والمسافة على منحنى بياني حيث البعد الأفقي يمثل قيم السرعة والبعد الشاقولي (العامودي) يمثل قيم المسافة سنجد أن الشكل الهندسي الناتج يتمثل بخط. فهذا الخط الذي ليس له نهاية أو بداية يوضح جميع قيم المسافة لأي قيمة سرعة؛ هذا يعني أنه وخلال زمنٍ محدد، في كل مرة تتغير السرعة سيحصل تغير في المسافة المقطوعة والعلاقة بينهما بهذه الحالة “خطية Linear”، ولهذا السبب ندعو المعادلة  السابقة  بين السرعة والمسافة هنا بمعادلة خطية Linear Equation، ويُسمى فرع الجبر الذي يهدف لدراسة العلاقات الخطية بين المتغيرات بالجبر الخطي Linear Algebra.

لكن ماذا لو كانت الحركة في المثال السابق لا تحدث فقط على خط مستوي x بل على خط جانبي y أيضا. يصبح للمركبة سرعة على الخط الجانبي v_y وسرعة على الخط المستوي v_x أي يتوجب علينا قياس المسافة على كلا الخطين .

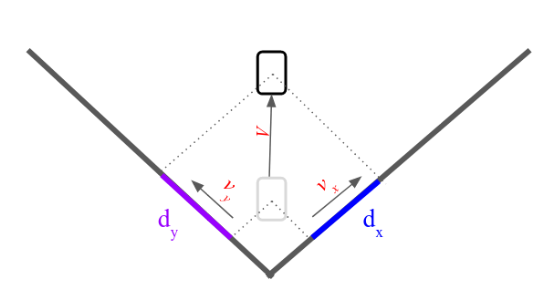
في هذه الحالة يصبح لدينا معادلة في كل اتجاه متعلقة بالسرعة في ذلك الاتجاه:

يمكننا كتابة المعادلات السابقة في طريقة مختصرة أكثر إذا ما مثلنا السرعة كمتجه (أو شعاع) vector يحتوي على متغير السرعة في كل اتجاه، ومتجه آخر للمسافة. بهذه الطريقة نرى أن المتجه V=(v_x,v_y) يحتوي على عناصر السرعة في كل اتجاه . نذكر من المثال السابق في حالة الحركة على خط مستوي أن متغير السرعى ينتمي إلى مجموعة الأعداد الحقيقية R، وبحالتنا هذه، يتكون متجه السرعة من مركبتين (أو عنصرين) كل منها تنتمي إلى مجموعة الأعداد الحقيقية، وبالتالي سيكون بإمكاننا تعريف المُتجه V ∈ ℝ² الذي ينتمي إلى المجموعة الناتجة عن الجداء الديكارتي للمجموعات التي تنتمي إليها عناصره أي ℝ x ℝ –> ℝ².

من السهل تعميم المثال السابق إلى الحالات التي يكون فيها المتغيرات ذي أبعاد تفوق البعد الواحد أو البعدين وبنفس المنطق من الممكن أن نمثل المتغيرات كمتجهات تنتمي إلى ℝ^N حيث N عدد طبيعي موجب. في تلك الحالة يصبح الشكل الهندسي الناتج عن المعادلات الخطية في البعد N ما يسمى بالمستوي الفائق Hyperplane.

• اقرأوا أيضاً: ما هو الفرق بين الذكاء الاصطناعي والبرمجة التقليدية؟

3. حل المعادلات

في المثال السابق تحدثنا عن المعادلات الخطية التي نعلم فيها جميع الثوابت التي تحدد العلاقة الخطية بين المتغيرات، (في المثال السابق الثابت كان Δt).  لكن ماذا لو كنا لا نعلم قيم تلك الثوابت أي لا نعلم العلاقة الرياضية بشكل كامل؟ ماذا لو حصلنا على مجموعة قيم لمتغير السرعة وقيم المسافة المناظرة لها. هل نستطيع أن نستنتج قيمة الثوابت في هذه الحالة. في المثال السابق الحل بسيط حيث نستنتج Δt بتقسيم المسافة على السرعة ولكن ماذا لو كانت المتغيرات عبارة عن متجهات ذات أبعاد عديدة؟ 

بهذه الحالة، أي عندما تكون المتغيرات هي متجهات (أو أشعة) ذات أبعادة عديدة، فإن العلاقة الخطية البسيطة السابقة التي تربط السرعة بالمسافة لن تكون كافية من أجل معرفة حالة المتغير؛ سنحتاج بهذه الحالة إلى تعريف نظام معادلات خطية يحتوي على M عدد من المعادلات وN عدد من المتغيرات. الهدف هو معرفة حلول هذه المعادلات عبر الوصول إلى قيم المتغيرات التي تجعل هذه المعادلات صحيحة (أي ذات حلول مقبولة وغير مستحيلة). نرمز لنظام المعادلات الخطية على الشكل التالي:

حيث A ∈ ℝ^MxN وb ∈ ℝ^N يمثلان المعطيات المعلومة عن المعادلات. يكون الطلب هنا أن نجد القيم المناسبة للمتجه x ∈ ℝ^N. وحسب قيم وأبعاد المعطيات قد يكون لنظام المعادلات حل وحيد، عدد لانهائي من الحلول أو لا يوجد فنقول أنها مستحيلة الحل. يوجد طرق مختلفة لحل المعادلات التي يتواجد لها حل أو أكثر، على سبيل المثال طريقة الحل بالتبديل، حل غاوس، حل كرامر الخ… لكننا سوف نهتم في هذا المقال إلى الحالة التي لا يتواجد لها حل.

في أغلب الحالات التي قد نهتم فيها في مجال مثل معالجة البيانات قد يكون لدينا عدد معادلات (أي بيانات) يفوق عدد المتغيرات المجهولة. في هذه الحالة نقول أن نظام المعادلات مفرط التحديد Over-determined System. أي من الصعب إيجاد حلول تستطيع إرضاء جميع المعادلات الكثيرة وهنا تكون مستحيلة الحل.

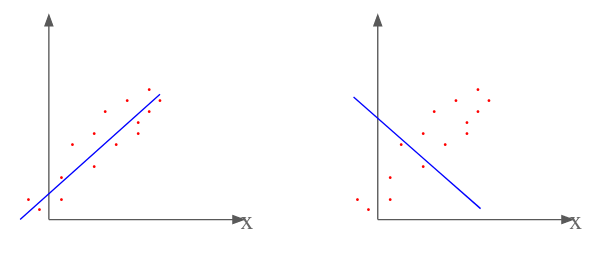
لكن عندما تكون مجموعة المعادلات مستحيلة الحل، من الممكن أن نقارب الحل. أي أن نجد قيم لـ x تعود إلينا بأقل كلفة ممكنة نسبة إلى تابع أو مقياس ما يحسب لنا جودة أي حل. بصيغة أبسط، في الحالة التي لا بتواجد فيها حل علينا حساب أقرب ما يمكن إلى ما قد يكون حل مناسب. لكن بصيغة رياضية أكثر نريد أن نجد ‘x حيث أن القيمة Ax’-b <= Ax-b ﻷي x آخر.

∃x’∈ ℝ^N such that ∀x ∈ ℝ^N , E[Ax’-b] <= E[Ax-b]

E تمثل القيمة المتوقعة Expected Value أي على معدل الخطأ أو الكلفة ل’x على جميع البيانات بالمجمل أن يكون أقل من معدل الخطأ لxعلى جميع البيانات.

• اقرأوا أيضاً: لماذا يستهلك الذكاء الاصطناعي الكثير من الطاقة؟

4. الجبر وتعلم اﻵلة

يعنى مجال تعلم اﻵلة Machine Learning بدراسة قواعد البيانات الهائلة والوصول إلى حلول تمكننا من استنتاج وفهم المعلومات عن بيانات مجهولة أو توقع أحداث عن تلك البيانات ما في المستقبل.

تعتمد نماذج تعلم الآلة بشكل كبير على الجبر كلغةٍ أساسية لوصف شكل وقيم البيانات، فضلاً عن اعتمادها – أي نماذج تعلم الآلة – على أسس مماثلة لوصف الحلول، وهذا يعني أنه وبشكلٍ مماثل لحل مجموعة معادلات جبرية ذات N متغير، يمكن صياغة مُشكلة معينة في تعلم الآلة كما يلي: بالنسبة لقاعدة بيانات x ∈ ℝ^MxN ومجموعة وسوم y ∈ ℝ^Mx1 علينا أن نجد متجه من المعطيات θ ∈ ℝ^Nx1 لتقليل قيمة تابع الكلفة cost.

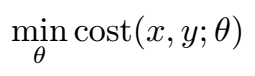
كيف يمكننا فهم ذلك؟ لو استرجعنا مبدأ عمل نماذج تعلم الآلة، لوجدنا أن النموذج يخضع في البداية لمرحلة تدريب (أو تعلم) بحيث يكون قادراً على فهم كيفية الوصول إلى حل المشكلة المطلوب ومن ثم تحسين أدائه عبر تكرار عمليات التدريب. يحتاج النموذج إلى بيانات دخل ترتبط بالمشكلة المطلوبة (وهي ما تم ترميزه بقاعدة البيانات x ∈ ℝ^MxN) كما يحتاج إلى وسوم تشير إلى الخرج المطلوب الوصول إليه (وهو ما تم ترميزه بالمتغير y ∈ ℝ^Mx1). ما يحصل في عملية التدريب هو أن بيانات الدخل والوسوم تكون معلومة، وما يجب معرفته هو متجه المعطيات θ، وهو ما يتم تدريب النموذج عليه. بالمقارنة مع حل المعادلات الجبرية، فإن متجه المعطيات هو قيم الثوابت a و b، وبحالة المعادلات الجبرية فإن هدفنا هو الوصول لقيم x التي تجعل المعادلة صحيحة. بحالة التعلم الآلي فإن الهدف هو الوصول لقيم الثوابت بعد معرفة الدخل (بهذه الحالة x) ومعلوماتٍ عن الخرج (أي الوسم y). بشكلٍ أكثر دقة، تهدف عملية تدريب نموذج تعلم الآلة على تدريبه ليكون قادراً على “التنبؤ” بقيم الثوابت التي ستؤدي للحل ذو الأرجحية الأعلى، ومع كل عملية تدريب سيتم تعديل قيم متجه المعطيات θ بما يؤدي لتحسين دقة النموذج في أداء المهمة المطلوبة منه.

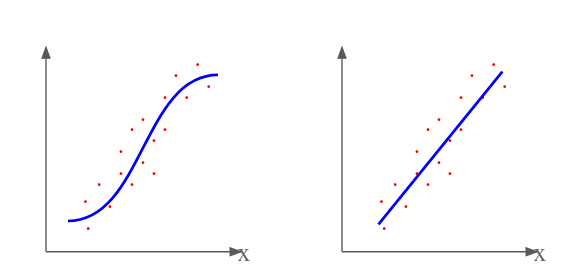
يُعتبر مبدأ المقاربة من أساسيات تعلم اﻵلة ﻷنه غالبا ما نتعامل مع أنظمة مفرطة التردد والطريقة التي نحسب فيها الكلفة مماثلة لنفس المبدأ في الجبر الخطي. في عدد من الحالات قد نحتاج إلى حل معقد أكثر من الحل الخطي كمنحني متعدد الخطوط. خوارزميات تعلم اﻵلة تمكننا من التوصل إلى حلول غير خطية وهذا مالا نستطيع فعله بالجبر الخطي فقط.

5. خلاصة

1. يمثل الجبر الخطي أحد الأدوات الرائعة التي يتيحها الرياضيات لنا لتمثل الظواهر المختلفة من حولنا بشكلٍ عددي قابل للحساب والحل
2. يمكن النظر إلى الذكاء الاصطناعي (بشكلٍ عام) وتعلم الآلة (بشكلٍ خاص) على أنها المجالات القائمة على إيجاد حلول لعددٍ كبير من المعادلات الرياضية
3. بدلاً من تحديد قيمة المتغيرات التي تجعل المعادلة (أو مجموعة المعادلات) ممكنة الحل، يتم تدريب نماذج تعلم الآلة من أجل التنبؤ بقيم الثوابت التي تؤدي لتنفيذ المهمة المطلوبة بأعلى أرجحية ودقة ممكنتين

6. مصادر إضافية للاطلاع

1. محاضرات غيلبرت سترانغ في الجبر الخطي في جامعة إم آي تي
2. سلسلة من قناة 3Blue1Brown عن الجبر الخطي